PARA LEER

En geometría, un polígono es una figura geométrica del plano, considerada como una sucesión finita de segmentos rectos consecutivos, tal que cada par de segmentos tiene, exactamente un punto común; también el primero con el último tienen un único punto común. Estos segmentos son llamados lados, y cada punto común a dos segmentos se llama vértice. El polígono es el caso bidimensional del politopo.

Definición

La definición del polígono depende del uso que se le quiera dar, así por ejemplo para hacer referencia a una región del plano se tiene:
  • Llamaremos polígono a la porción del plano delimitada y encerrada por una línea poligonal.4​
Para hacer referencia al estudio euclidiano de las longitudes de los lados de un polígono, se tiene:
  • Llamaremos polígono a una figura geométrica plana definida por una línea poligonal de la cual sus dos extremos coinciden.
Para desarrollar un concepto didáctico del polígono, se tiene:
  • Llamaremos polígono al conjunto de puntos y segmentos que unen sucesivamente dichos puntos.
En esta última definición se suele evitar los puntos consecutivos alineados.


Elementos de un polígono[editar]

Plantilla00.svgResultado de imagen para paisajes con poligonos
En un polígono se distinguen los siguientes elementos geométricos:
  • Lados del polígono: son cada uno de los segmentos que conforman el polígono.
  • Vértices de un polígono: son los puntos de intersección o puntos de unión entre lados consecutivos.
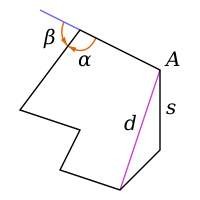
  • Diagonales del polígono: son segmentos que une dos vértices, no consecutivos, del polígono.
  • Ángulo interior del polígono: es el ángulo formado, internamente al polígono, por dos lados consecutivos.
  • Ángulo exterior del polígono: es el ángulo formado, externamente al polígono, por uno de sus lados y la prolongación del lado consecutivo.
  • Ángulo entrantes del polígono: es el ángulo interior al polígono que miden más de 180º.8​
  • Ángulo salientes del polígono: es el ángulo interior al polígono que miden menos de 180º.9​

Hexágono regular.
En un polígono regular se puede distinguir, además:
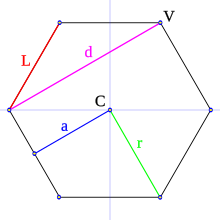
  • Centro (C): es el punto equidistante de todos los vértices y lados.
  • Ángulo central (AC): es el ángulo formado por dos segmentos de recta que parten del centro a los extremos de un lado.
  • Apotema (a): es el segmento que une el centro del polígono con el centro de un lado; es perpendicular a dicho lado.
  • Diagonal (): son los segmentos que unen los vértices del polígono no consecutivamente

Comentarios

Publicar un comentario

Entradas populares de este blog

PARA HACER

Imagen
1. Dibuje los siguientes polígonos regulares y trace sus elementos 2. Elija un polígono de lado mayor de 10 , halle sus elementos y sustente lo ante sus compañeros Clasificación de polígonos según el número de lados Nombre n.º lados trígono  o  triángulo 3 tetrágono ,  cuadrángulo  o  cuadrilátero 4 pentágono 5 hexágono 6 heptágono 7 octógono  u  octágono 8 eneágono  o  nonágono 9 decágono 10 endecágono  o  undecágono 11 dodecágono 12 tridecágono 13 tetradecágono 14 pentadecágono  o  pentedecágono 15 hexadecágono 16 heptadecágono 17 octodecágono  u  octadecágono 18 eneadecágono  o  nonadecágono 19 isodecágono  o  icoságono 20 icosakaidígono 22 triacontágono 30 tetracontágono 40 pentacontágono 50 hexacontágono 60 heptacontágono 70 octocontágono u octacontágono 80 eneacontágono o nonacontágono 90 hectágono 100 chiliágono 1000 miriágono 10000 decemir...
Leer más

POLÍGONOS

Imagen
En  geometría , un   polígono  es una  figura geométrica  del plano, considerada como una sucesión finita de  segmentos rectos  consecutivos, tal que cada par de segmentos tiene, exactamente un punto común; también el primero con el último tienen un único punto común. Estos segmentos son llamados lados, y cada punto común a dos segmentos se llama vértice. El polígono es el caso  bidimensional  del  politopo . Definición La definición del  polígono  depende del uso que se le quiera dar, así por ejemplo para hacer referencia a una región del plano se tiene: Llamaremos polígono a la porción del plano delimitada y encerrada por una línea poligonal. 4 ​ Para hacer referencia al estudio euclidiano de las longitudes de los lados de un polígono, se tiene: Llamaremos polígono a una figura geométrica plana definida por una línea poligonal de la cual sus dos extremos coinciden. Para desarrollar un concepto didáctic...
Leer más

PARA EVALUAR

Imagen
ADIVINA QUIEN SOY !!  Contesta cada adivinanza. Luego, dibuja la figura en el espacio de la derecha con un reglón. 1. Soy un cuadrángulo. Tengo 2 pares de lados paralelos. Todos mis ángulos son rectos. No soy un cuadrado. ¿Qué soy? 2. Soy un polígono. Todos mis lados tienen la misma medida. Todos mis ángulos tienen la misma medida. Tengo 3 lados. ¿Qué soy? 3. Soy un polígono. Soy un cuadrángulo. Todos mis lados tienen la misma longitud. Ninguno de mis ángulos es recto. ¿Qué soy? 
Leer más